Day: July 5, 2014

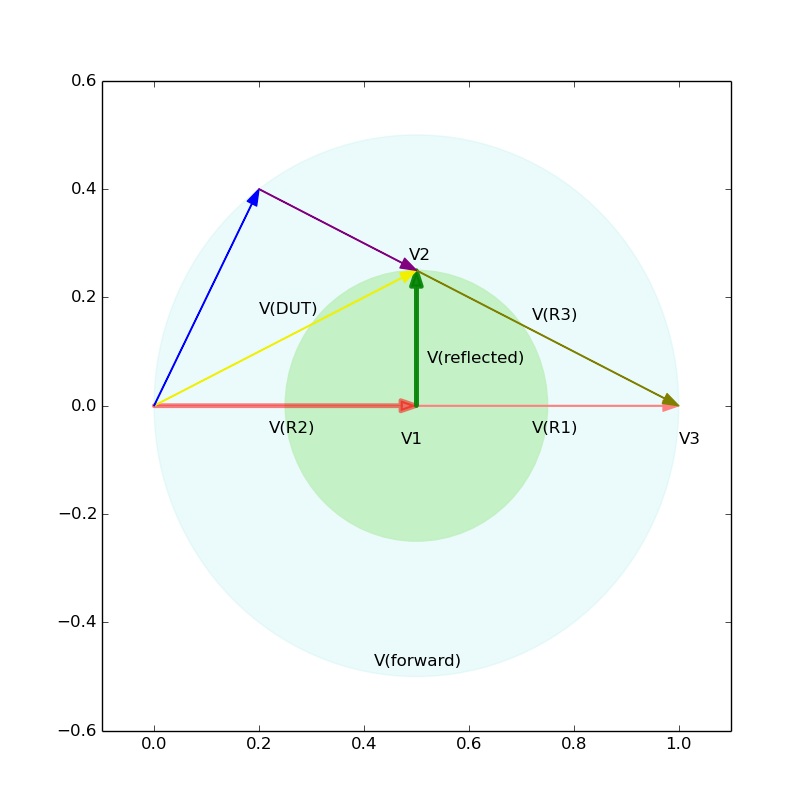
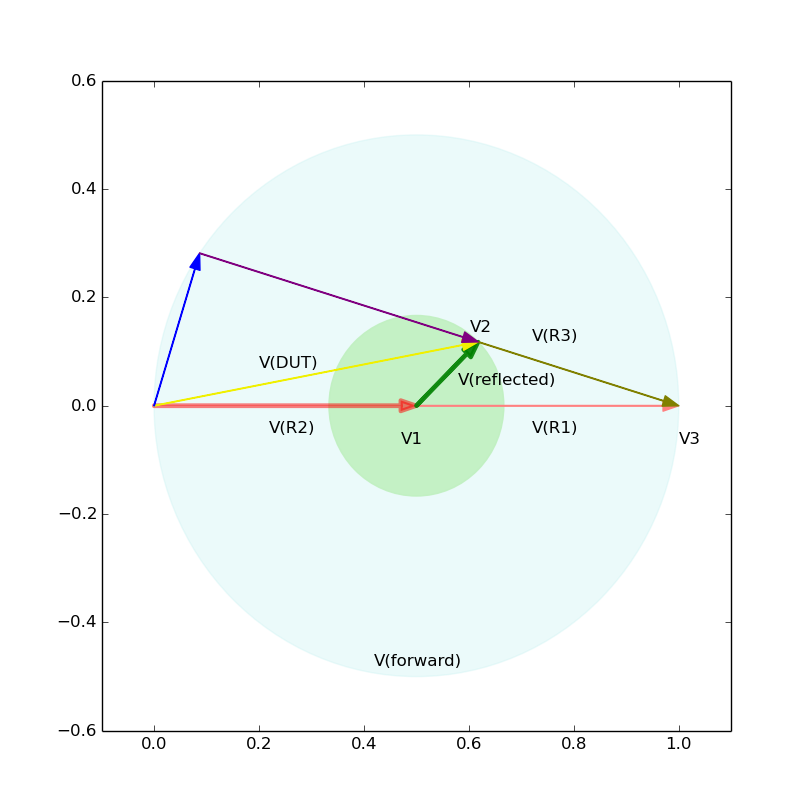
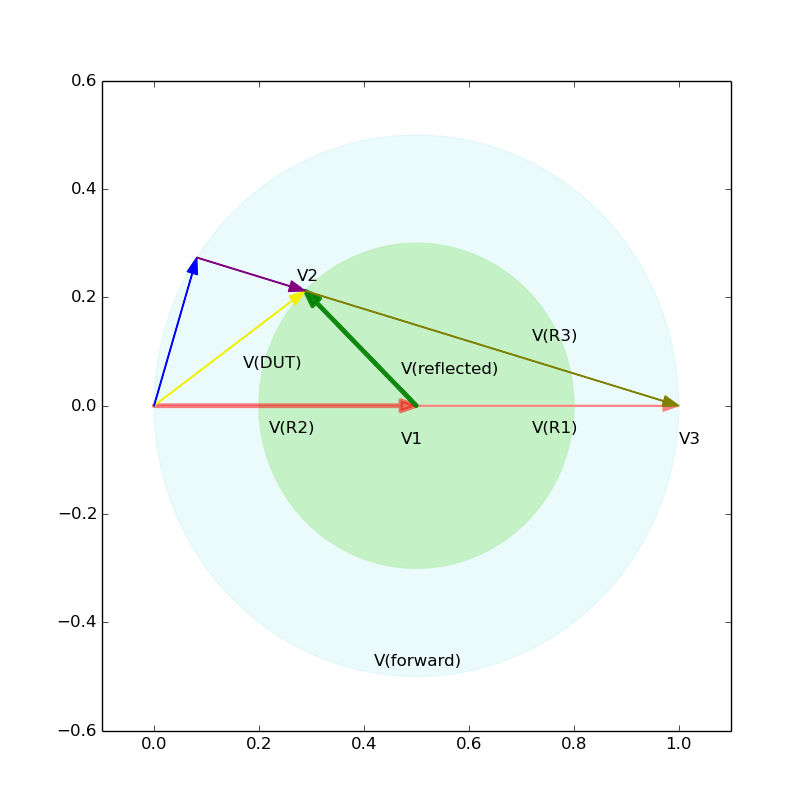
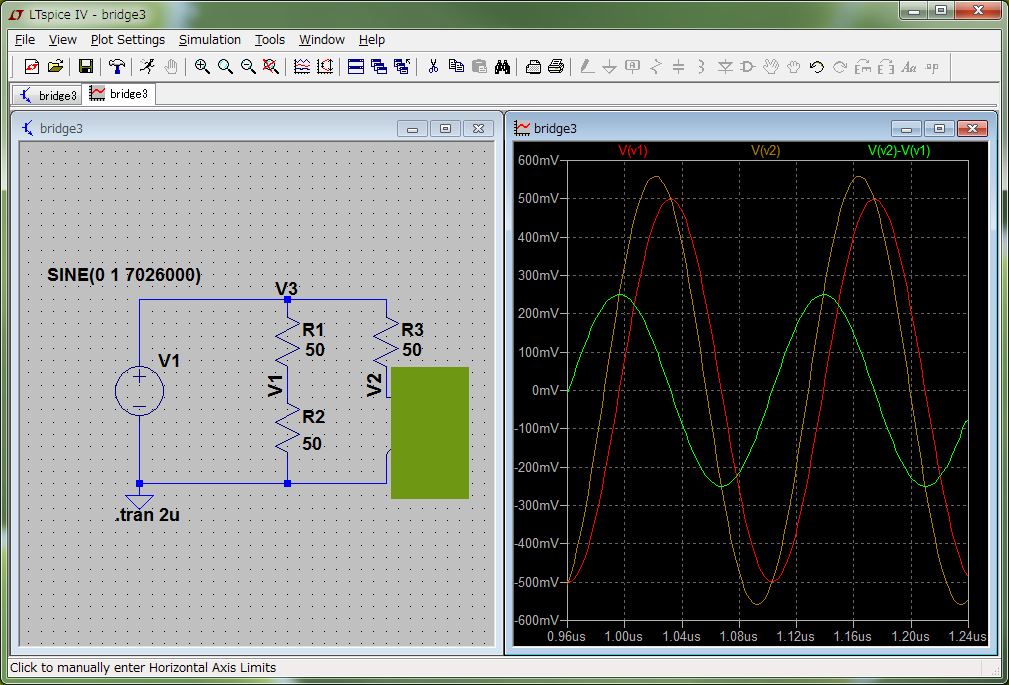
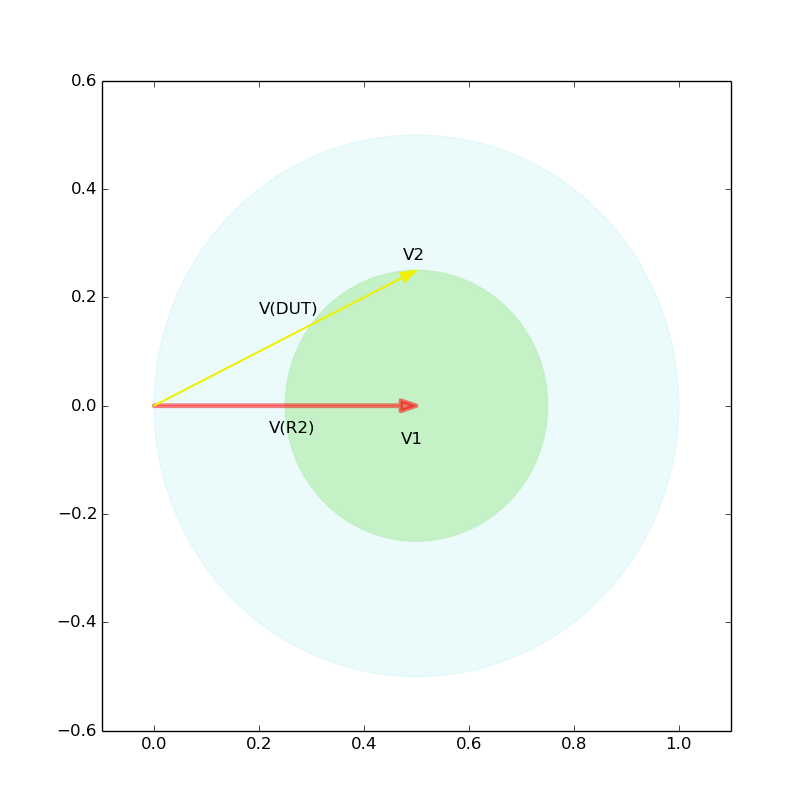
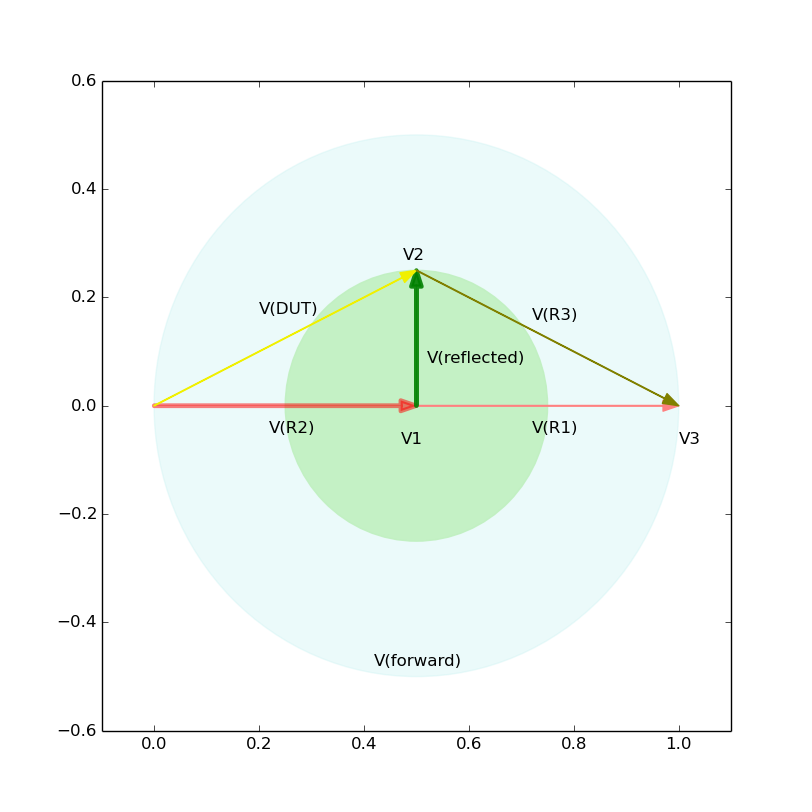
Now let us graphically obtain Z(DUT) for three cases. Note that the reflection coefficient, gamma, is a complex number defined as V(reflected)/V(forward). I forgot to annotate V(R2) as V(forward). Please see, for example, this figure.

This is the case in which abs(gamma)=1/2 and arg(gamma)=90 deg. We see graphically, or by measuring the length of each vector, that Z(DUT)=40 + j30 [ohm]. Note that since abs(gamma)=0.5, VSWR=(1+abs(gamma))/(1-abs(gamma))=3.

Next, this is the case abs(gamma)=1/3 and arg(gamma)=45 deg. Again, we see graphically that Z(DUT)=69.5 + j36.8 [ohm], and VSWR=(1+1/3)/(1-1/3)=2.

Finally, this is the case abs(gamma)=3/5 and arg(gamma)=135 deg. We see that Z(DUT)=14.5 + j19.2 [ohm], and VSWR=(1+3/5)/(1-3/5)=4.

Notice that the length of V(R3) differs in three figures, although the length corresponds to 50 [ohm] in each case.

Now, here is the fun part.

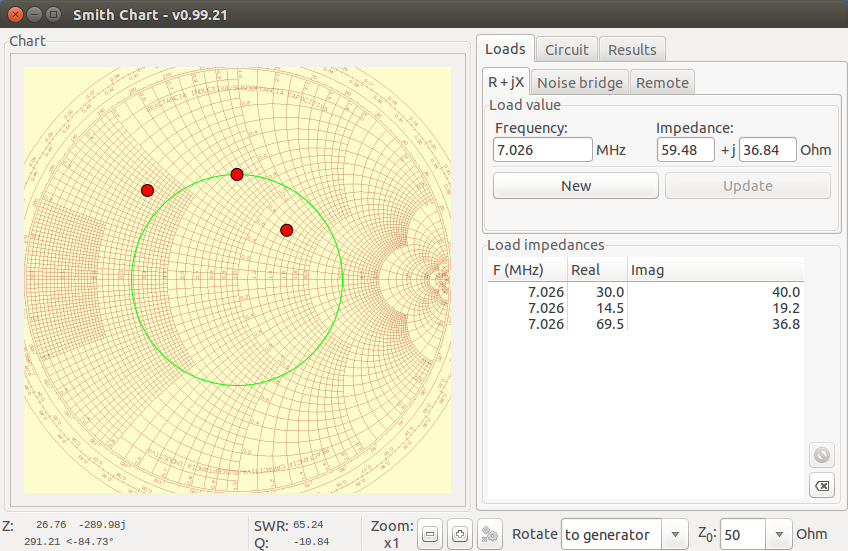
Let’s see the Smith Chart with three Lord impedances, which are the Z(DUT)s in the three cases. (Note the green circle is a SWR=3 circle.)

Do you see how these three red points in the Smith Chart relate to the three vector diagrams above? Yes, the red pionts are the end points of the vector V(reflected).

So if you observe V1 and V2 with your oscilloscope and draw a vector V(reflected), or equivalently a vector V(DUT) on a Smith Chart, you will directly get Z(DUT) just by reading a chart. Cool?

Now you understand that if you observe two waveforms V1 and V2 with your impedance bridge, you will obtain Z(DUT) after some simple calculations, which you can do it manually or with a short program as is shown in my previous post, Eureka.

But, how can you do it painlessly, assuming that you do not like calculations very much, by just drawing a vector diagram? Here is the answer, namely a graphical solution:

First, you draw two vectors V(R2) and V(DUT), which you observed as V1 and V2, respectively. In this example, V2/V1=1.118 and at V2 is advanced in relative to V1 with 26.56 deg. This is all the information you need to get Z(DUT), but you can add some more vectors to fully understand the situation with your bridge.

First, you will immediately notice that by symmetry of the diagram, the length of V(DUT) is equal to that of V(R3), and since R3=50 [ohm] and the same current goes through both the DUT and R3, abs(Z(DUT)) is also 50 [ohm], which means R^2+X^2=50 [ohm], where R and X are defined as Z(DUT)=R+jX.

Now, the next step is to determine R and X.

For that, you will decompose the vector V(DUT) into two orthogonal vectors, the blue and the purple, by extending the vector V(R3) until it hits the outer circle. Then the length of the blue vector tells you how large X is, and the purple, R.

Noting that R3 is 50 [ohm], you will know that R (purple) is 30 [ohm] and X (blue) is 40 [ohm]

Are you sure that Z(DUT)=30+j40 [ohm]? Can you tell by just observing the waveforms?

Let’s check with a python program.

# given waveforms
t=arange(0,1000)
v1=1.0*sin(t*(2.0*np.pi/444.0)+0.0)
v2=sqrt(5.0)/2.0*sin(t*(2.0*np.pi/444.0)+math.atan(1.0/2.0))
# Note that sqrt(5.0)/2.0=1.118 and atan(1.0/2.0)=26.56deg.

# start computing
z0=50.0+0.0j
cv1=1.0+0.0j
cv2=vratio*(cos(phase2advance)+sin(phase2advance)*1.0j)
cvr=2.0*cv1-cv2
cz=z0*(cv2/cvr)
gamma=(cz-z0)/(cz+z0)
swr=(1+abs(gamma))/(1-abs(gamma))

print "vratio=", vratio
print "phase2advance=", phase2advance*360.0/(2.0*np.pi)
print "Z(DUT)=", cz
print "gamma=",gamma
print "swr=", swr

And the results are:

vratio= 1.11803398875
phase2advance= 26.5650511771
Z(DUT)= (30+40j)
gamma= (-1.02119201983e-13+0.5j)
swr= 3.0

So you are correct!

Actually, the DUT was 30 [ohm] + 909.5 [nH], which is at 7026kHz 30 [ohm] + j40 [ohm].