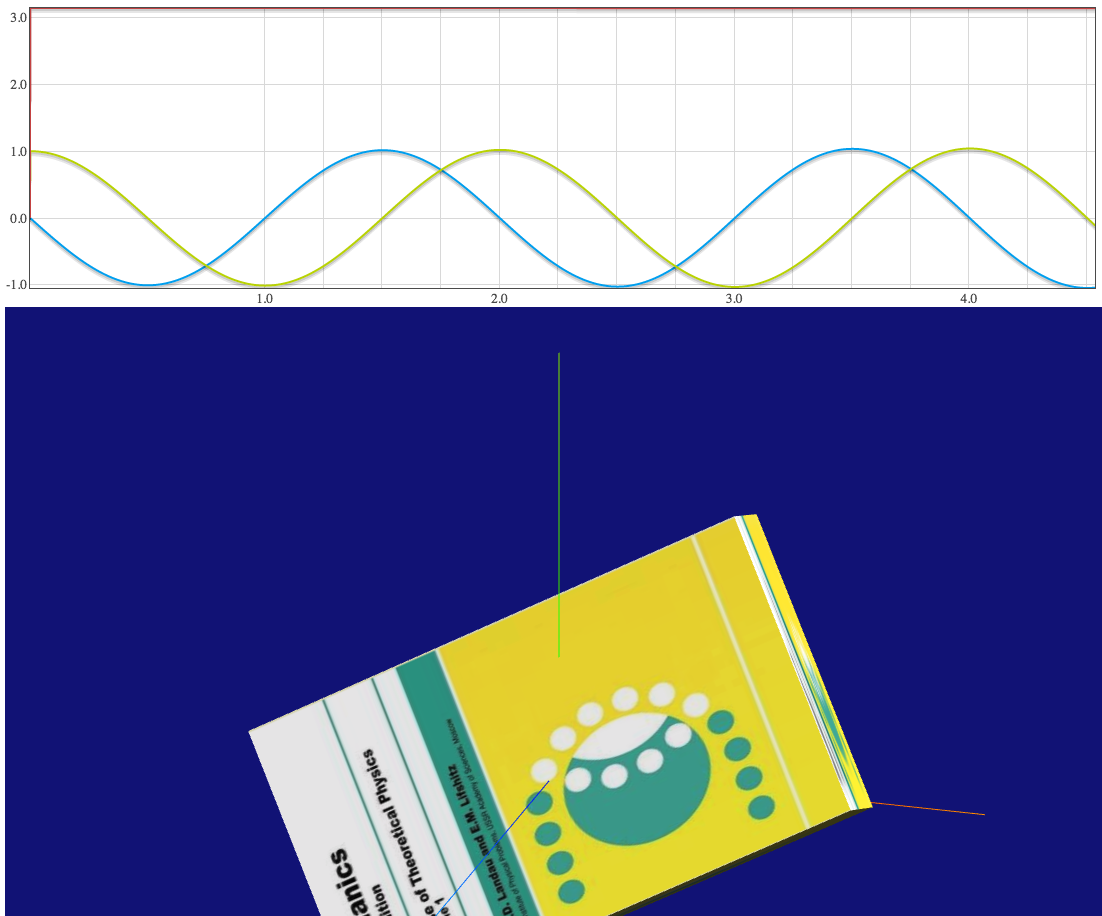
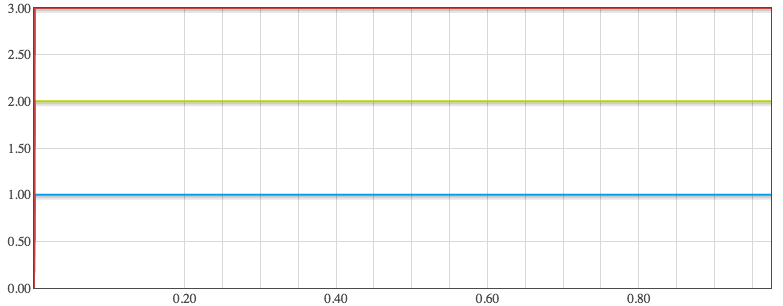
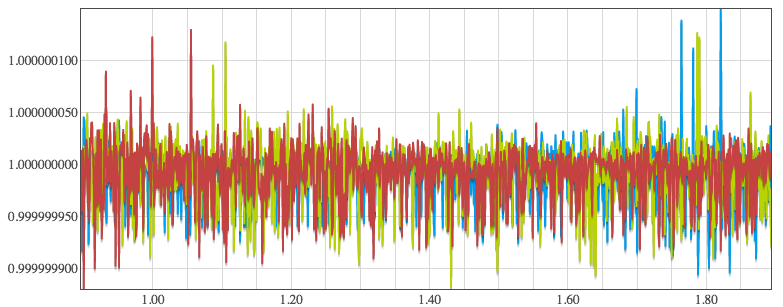
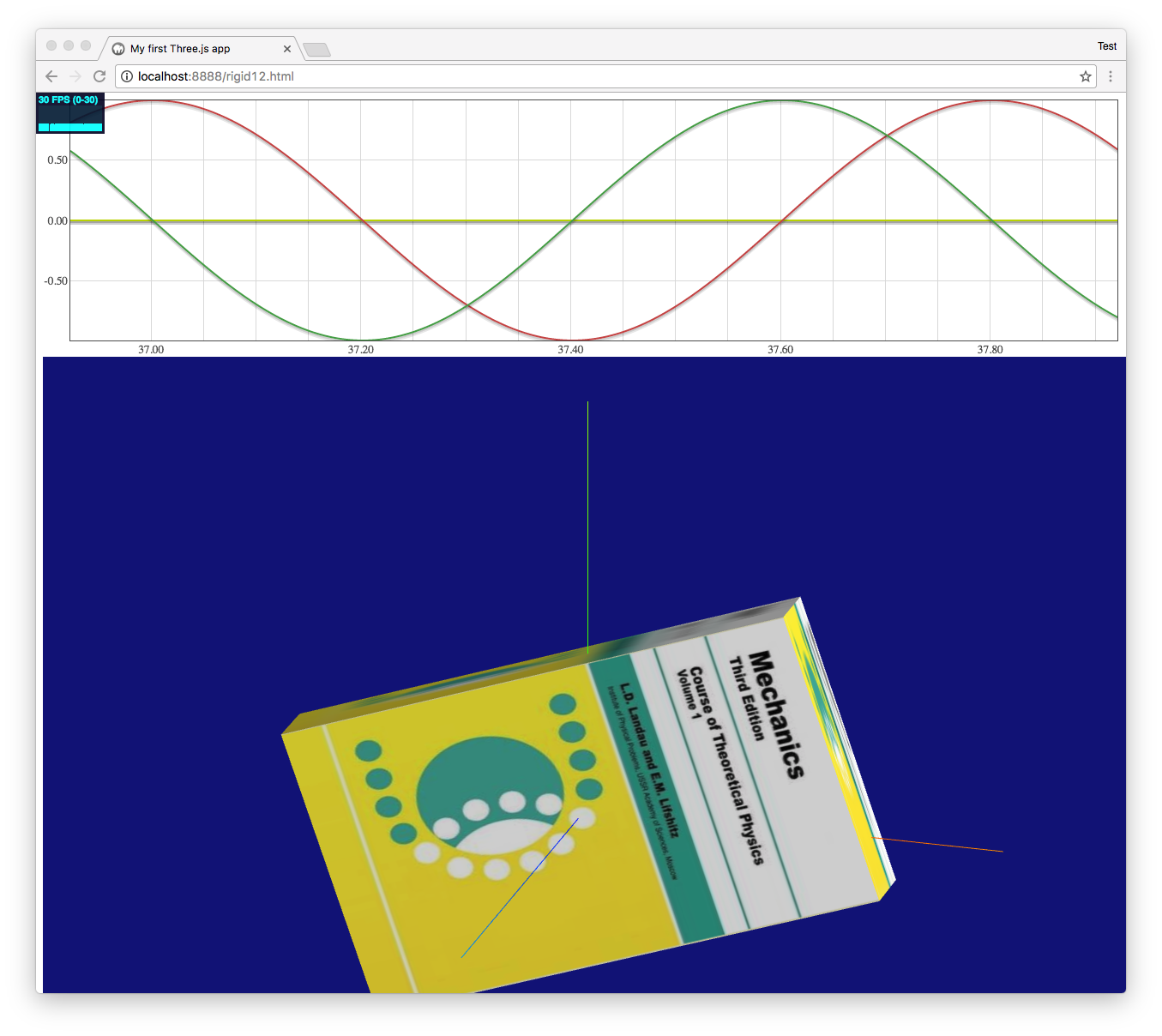
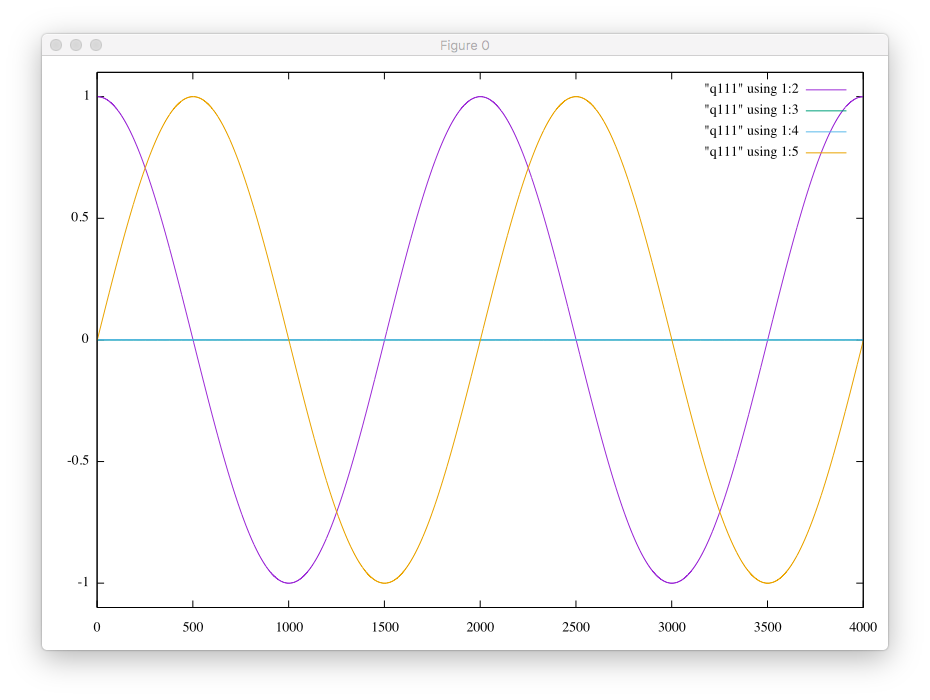
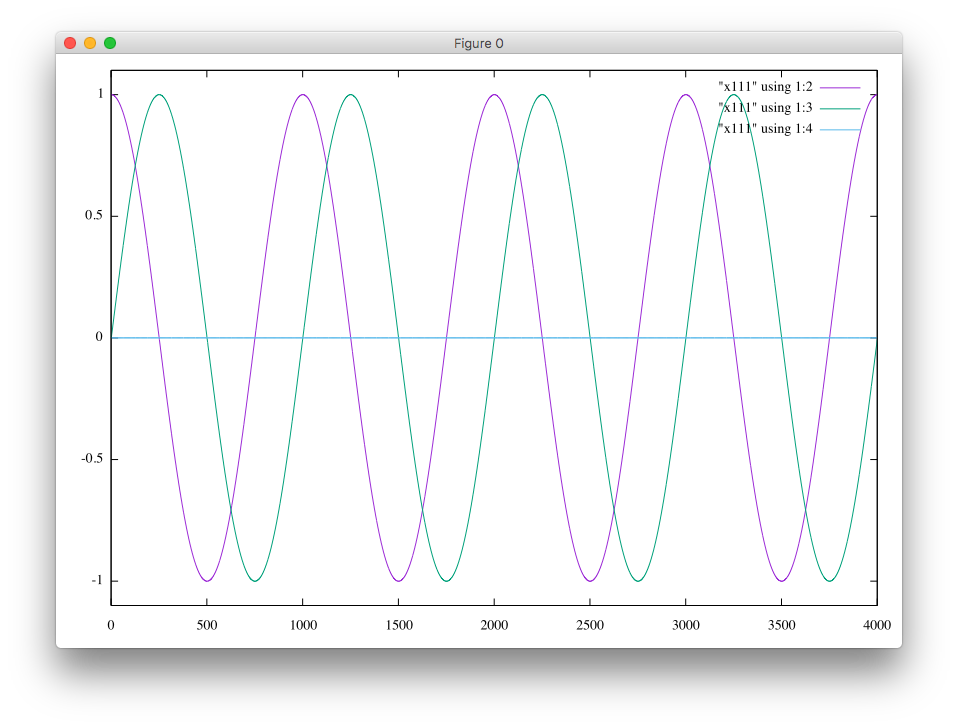
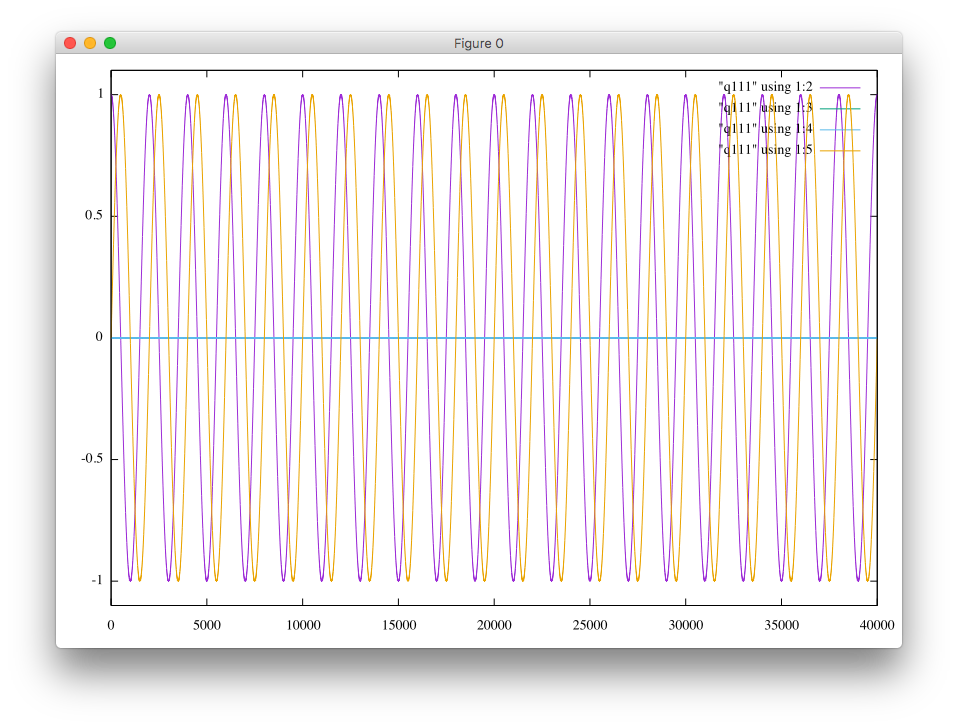
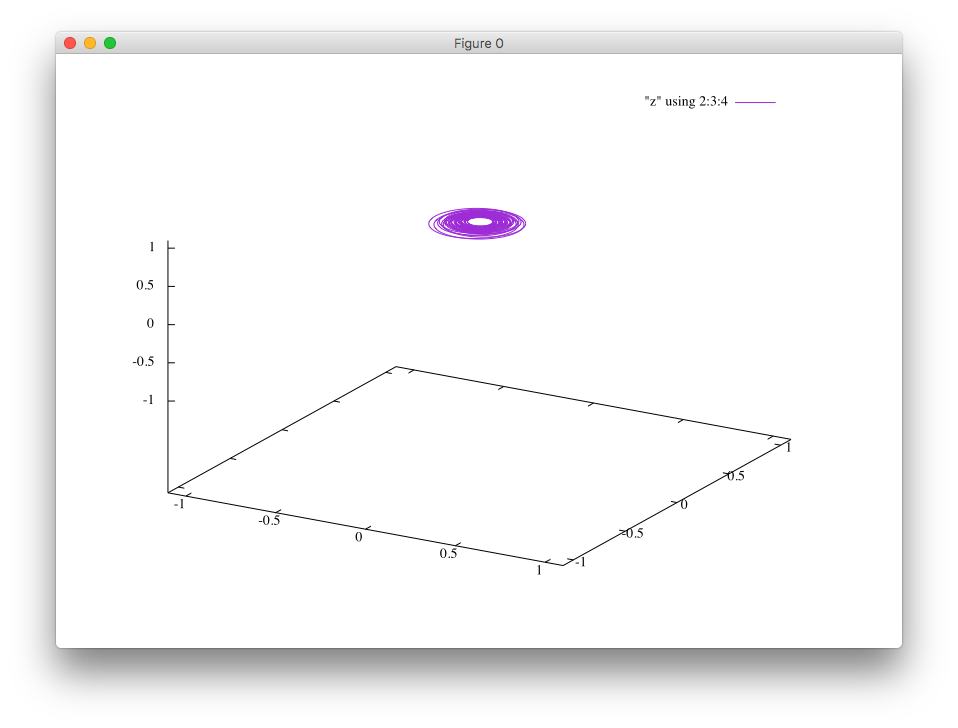
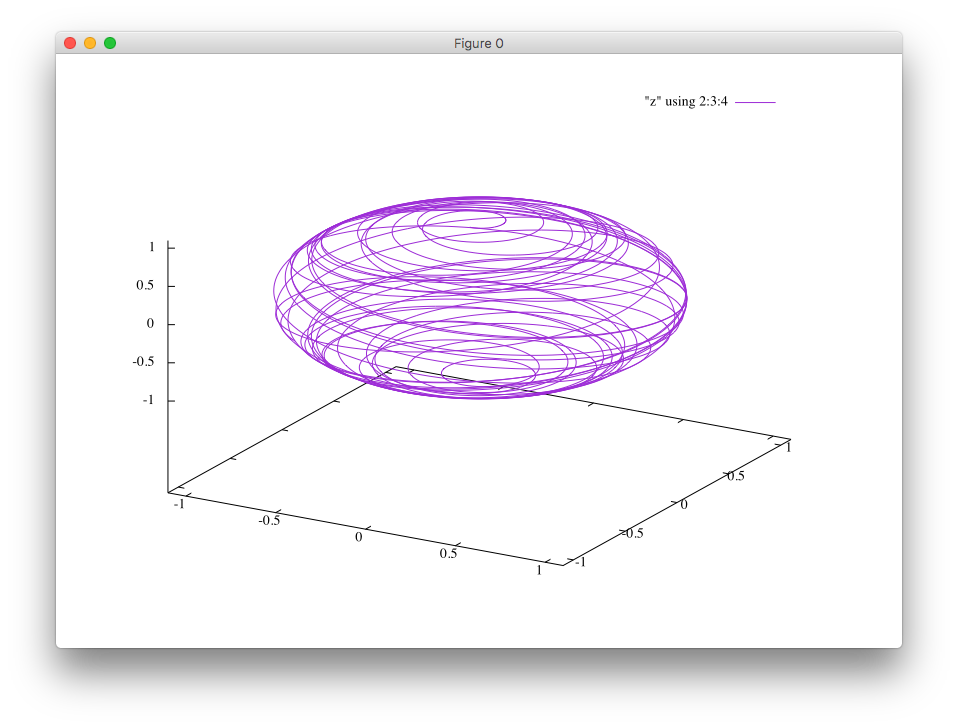
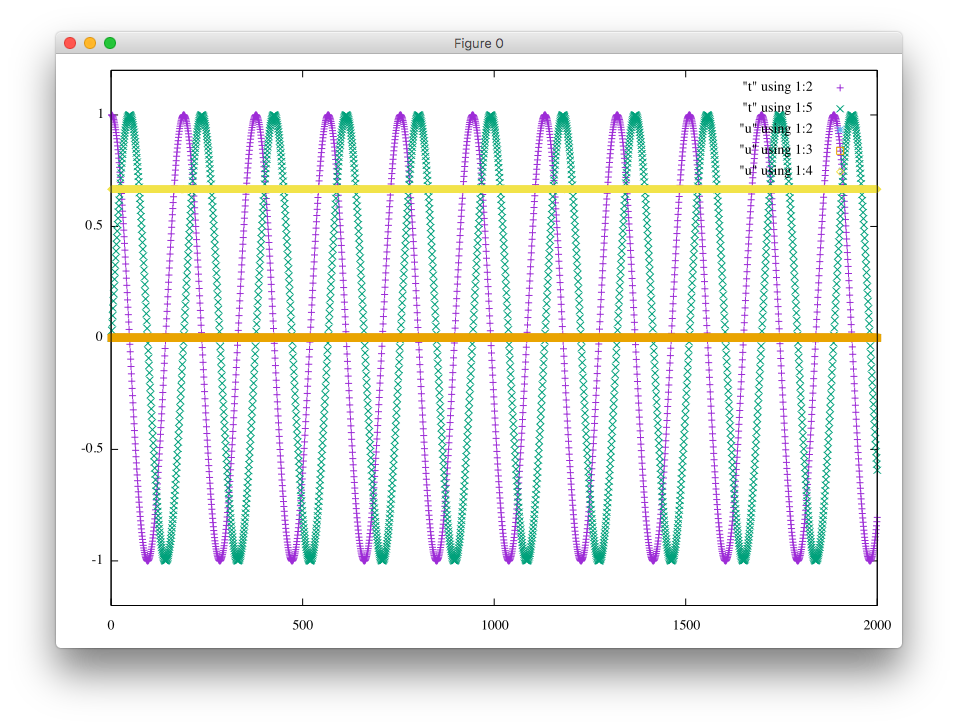
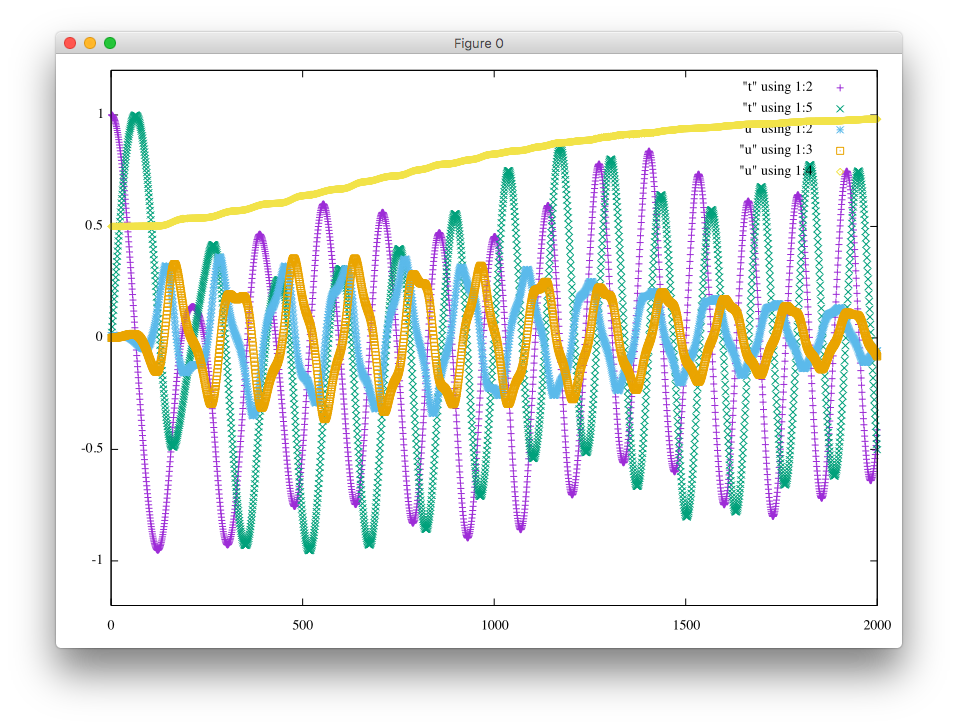
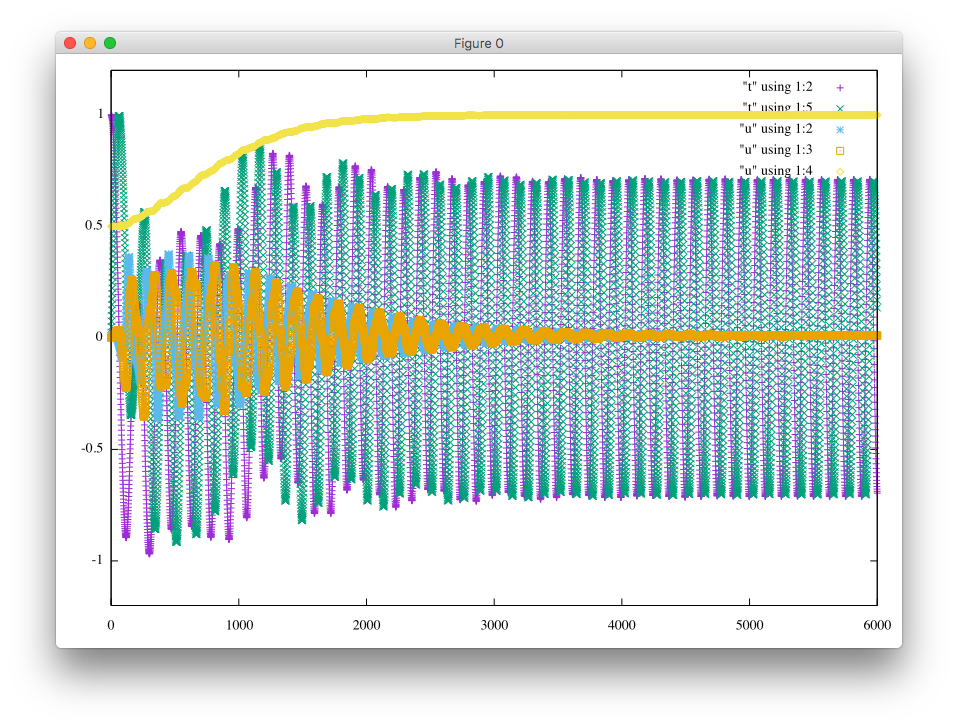
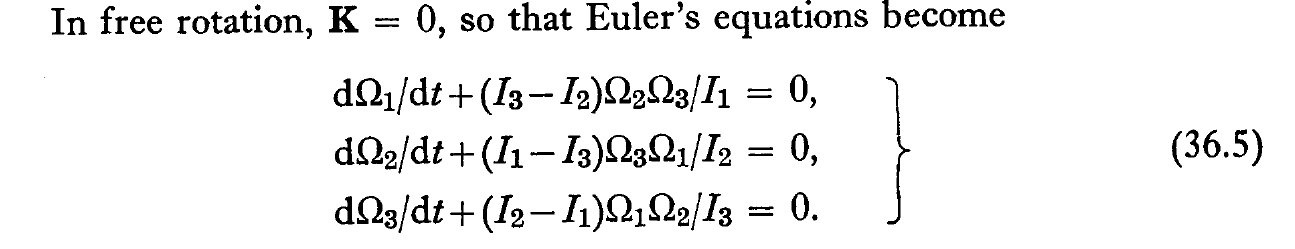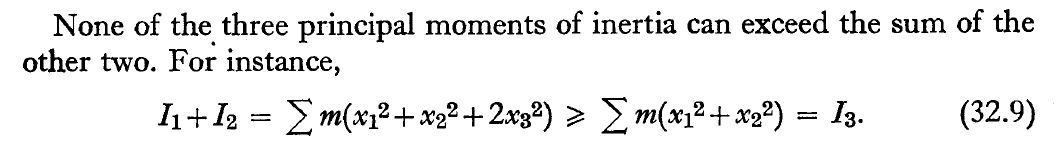Please click either an unstable case or a stable case.
The source code may include some errors, bat basically it seems to be OK. I am not sure if I really have to write functions matrix4_from_matrix3() and matrix3_from_matrix4().
Please check the following documents, if you are in doubt.
https://threejs.org/docs/api/math/Vector3.html
https://threejs.org/docs/api/math/Quaternion.html
https://threejs.org/docs/api/math/Matrix3.html
https://threejs.org/docs/api/math/Matrix4.html
<html>
<head>
<title>My first Three.js app</title>
<style>
body { margin: 0; }
canvas { width: 100%; height: 100% }
</style>
</head>
<body>
<script src="https://ajax.googleapis.com/ajax/libs/threejs/r76/three.min.js"></script>
<script>
function matrix4_from_matrix3 (m4, m3) {
var se = m3.elements;
var te = m4.elements;
te[0] = se[0]; te[4] = se[3]; te[ 8] = se[6]; te[12] = 0;
te[1] = se[1]; te[5] = se[4]; te[ 9] = se[7]; te[13] = 0;
te[2] = se[2]; te[6] = se[5]; te[10] = se[8]; te[14] = 0;
te[3] = 0; te[7] = 0; te[11] = 0; te[15] = 0;
}
function matrix3_from_matrix4 (m3, m4) {
var se = m4.elements;
var te = m3.elements;
te[0] = se[0]; te[3] = se[4]; te[6] = se[ 8];
te[1] = se[1]; te[4] = se[5]; te[7] = se[ 9];
te[2] = se[2]; te[5] = se[6]; te[8] = se[10];
}
var scene = new THREE.Scene();
var camera = new THREE.PerspectiveCamera(7, window.innerWidth/window.innerHeight, 0.1, 1000 );
var renderer = new THREE.WebGLRenderer();
renderer.setSize( window.innerWidth, window.innerHeight );
document.body.appendChild( renderer.domElement );
var geometry = new THREE.BoxGeometry( 4, 9, 1 );
var material2= new THREE.MeshLambertMaterial( { color: 0xf01010 } );
var cube= new THREE.Mesh( geometry, material2 );
cube.position.x = 0.0;
scene.add( cube );
var geometry0= new THREE.BoxGeometry( 1000, 1000, 1);
var material0 = new THREE.MeshBasicMaterial( { color: 0x101040 } );
var cube0 = new THREE.Mesh( geometry0, material0 );
cube0.position.z = -10;
scene.add( cube0 );
camera.position.x = 100;
camera.position.y = 100;
camera.position.z = 250;
camera.lookAt(cube.position);
scene.add( camera );
var light = new THREE.DirectionalLight(0xffffff);
light.position.set(250, 250, 250);
scene.add( light );
var light0 = new THREE.AmbientLight( 0x404040 );
scene.add( light0 );
var Ibody = new THREE.Matrix3();
var IbodyInv = new THREE.Matrix3();
var IbodyInv4 = new THREE.Matrix4();
Ibody.set(82,0,0, 0,17,0, 0,0,97);
IbodyInv.getInverse(Ibody);
matrix4_from_matrix3 (IbodyInv4, IbodyInv);
var q = new THREE.Quaternion();
var qq = new THREE.Quaternion();
var qdot = new THREE.Quaternion();
var axis = new THREE.Vector3(0,1,0).normalize();
var angle = Math.PI * 0.0;
q.setFromAxisAngle(axis,angle);
var x, y, z, w;
var L = new THREE.Vector3();
var L4 = new THREE.Vector4();
L.set(13.0*2.0*Math.PI*82.0,2.0*Math.PI*0.1,2.0*Math.PI*0.1);
L4.set(L.x, L.y, L.z, 0);
var omega = new THREE.Vector3();
var R = new THREE.Matrix3();
var RInv = new THREE.Matrix3();
var IInv = new THREE.Matrix3();
var R4 = new THREE.Matrix4();
var RInv4 = new THREE.Matrix4();
var IInv4 = new THREE.Matrix4();
var dt = 0.001;
var render = function () {
requestAnimationFrame( render );
x = q.x; y = q.y; z = q.z; w = q.w;
R.set(1.0-2.0*y*y-2.0*z*z, 2.0*x*y+2.0*w*z, 2.0*x*z-2.0*w*y,
2.0*x*y-2.0*w*z, 1.0-2.0*x*x-2.0*z*z, 2.0*y*z+2.0*w*x,
2.0*x*z+2.0*w*y, 2.0*y*z-2.0*w*x, 1.0-2.0*x*x-2.0*y*y);
RInv.getInverse(R);
matrix4_from_matrix3 (R4 , R );
matrix4_from_matrix3 (RInv4, RInv);
// IInv = R * IbodyInv * RInv;
IInv4.multiplyMatrices(R4, IbodyInv4);
IInv4.multiply (RInv4);
matrix3_from_matrix4 (IInv, IInv4);
// omega = IInv * L;
omega.copy(L);
omega.applyMatrix3(IInv);
qq.set(omega.x/2.0, omega.y/2.0, omega.z/2.0, 0.0);
// qdot = qq * q;
qdot.multiplyQuaternions(qq, q);
// q += qdot * dt;
q.set(q.x+qdot.x*dt, q.y+qdot.y*dt, q.z+qdot.z*dt, q.w+qdot.w*dt);
q.normalize();
cube.rotation.setFromQuaternion(q);
renderer.render(scene, camera);
}
render();
</script>
</body>
</html>