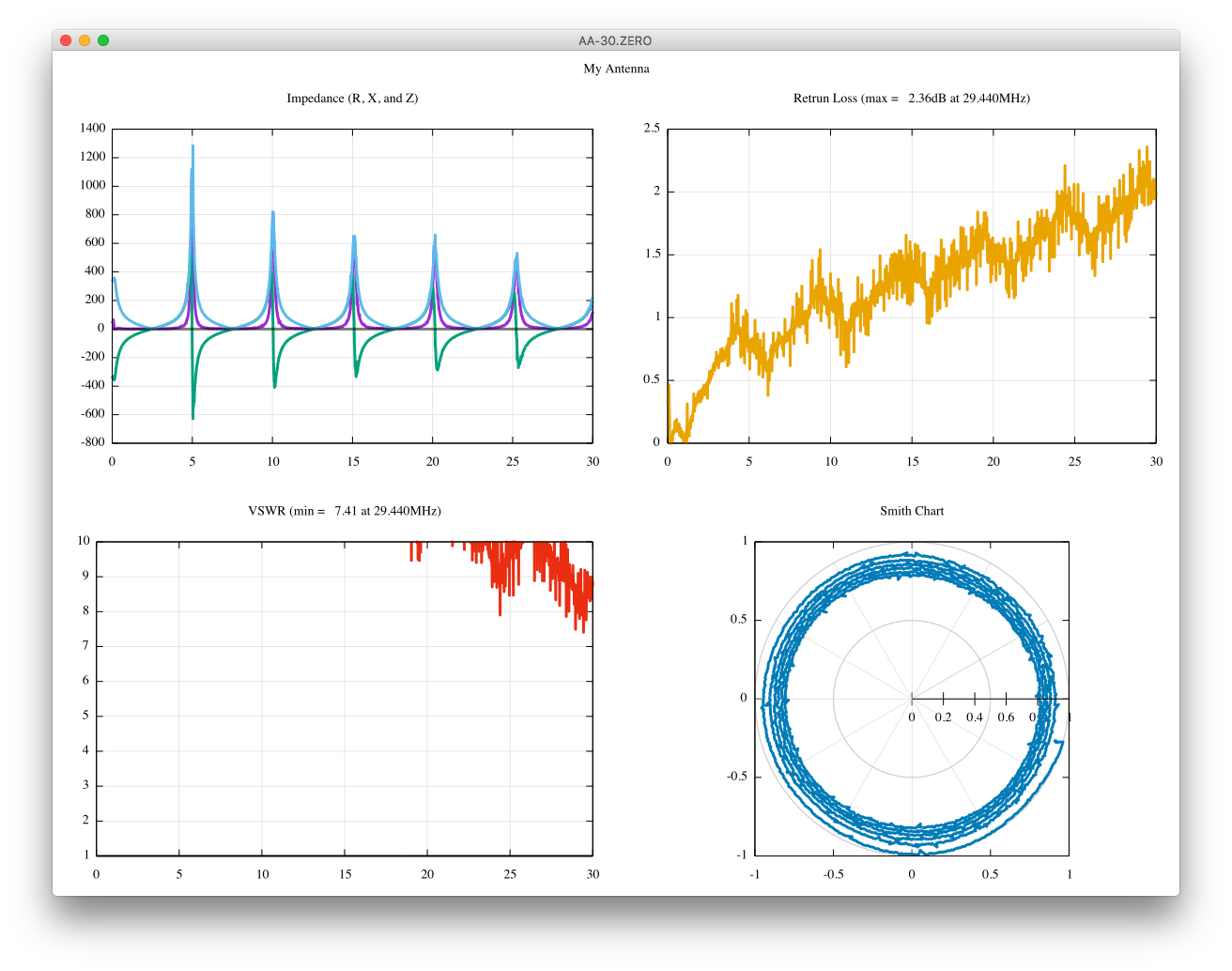
私は20mの同軸ケーブル(5D-2V)を使っていますが、測定の最中はケーブルの遠端は開放にしておきます。
スミスチャートはあなたに全てを告げますが、それでも、振幅と位相とを別々に見た方が容易でしょう。
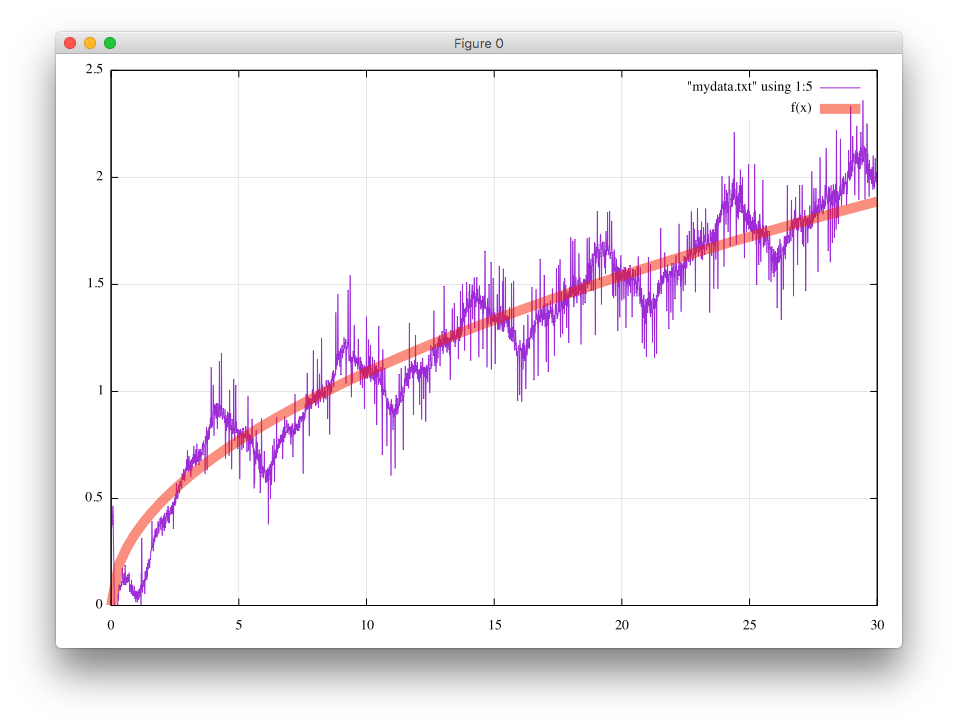
最初に、dBで表した振幅です。
% gnuplot gnuplot> f(x)=a*sqrt(x) gnuplot> fit f(x) "mydata.txt" using 1:5 via a iter chisq delta/lim lambda a 0 9.0593050625e+02 0.00e+00 8.02e-01 2.070472e-01 1 5.4539304323e+01 -1.56e+06 8.02e-02 3.445278e-01 2 5.4539209850e+01 -1.73e-01 8.02e-03 3.445736e-01 iter chisq delta/lim lambda a After 2 iterations the fit converged. final sum of squares of residuals : 54.5392 rel. change during last iteration : -1.7322e-06 degrees of freedom (FIT_NDF) : 3000 rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 0.134832 variance of residuals (reduced chisquare) = WSSR/ndf : 0.0181797 Final set of parameters Asymptotic Standard Error ======================= ========================== a = 0.344574 +/- 0.0006355 (0.1844%) gnuplot> print a*sqrt(30) 1.88730727013936
30MHzでの損失1.887[dB]は、公称値の0.44dB/10m、すなわち、1.76dB/40mと良く一致します。
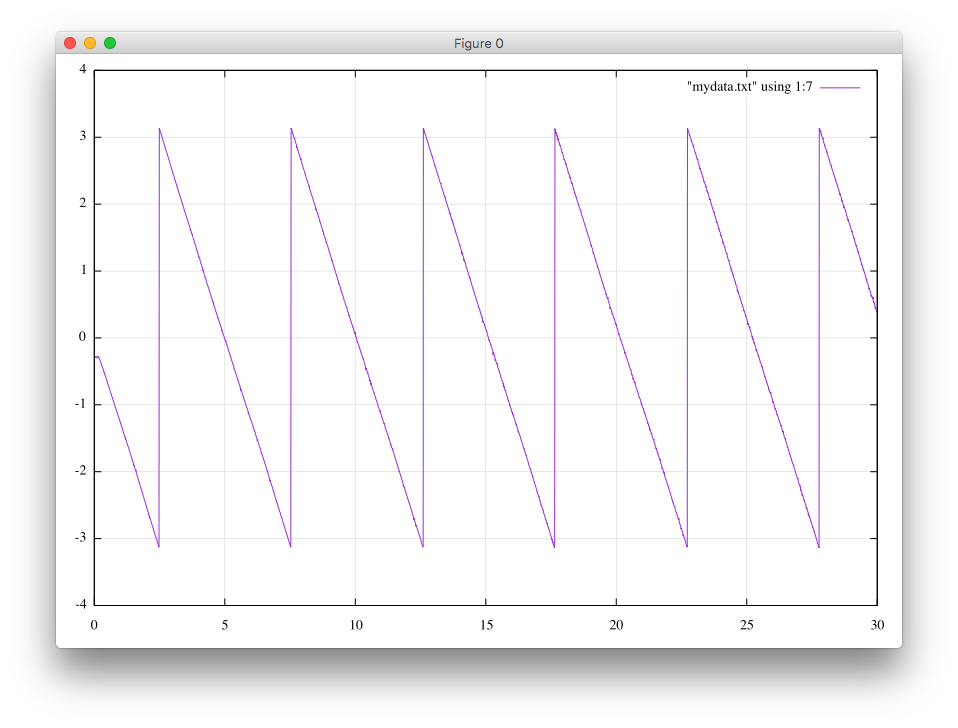
次に、ラジアンで表した位相です。
位相がマイナスπから、プラスπに変化する周波数を見てみましょう。
2.48, 1.3514, -0.299513, 1.3842, 0.469624, 36.9999, -3.1296, 0.947368 2.49, 1.39451, 0.083306, 1.397, 0.484627, 35.8549, 3.13826, 0.945733 7.53, 2.59869, -0.289392, 2.61476, 0.903662, 19.2411, -3.12999, 0.901191 7.54, 2.45728, 0.08333, 2.4587, 0.854434, 20.3477, 3.13825, 0.906313 12.6, 3.4673, -0.351551, 3.48508, 1.20654, 14.4212, -3.12746, 0.870308 12.61, 3.43064, 0.097069, 3.43201, 1.1938, 14.5746, 3.13769, 0.871586 ... 27.77, 5.43172, -0.091826, 5.43249, 1.89464, 9.20522, -3.13788, 0.804022 27.78, 5.31208, 0.100171, 5.31302, 1.85259, 9.41255, 3.13754, 0.807924
周期は (27.77MHz-2.48MHz)/5cyles、すなわち、5.06MHz/cycleです。
従ってケーブルの電気長は、(300m*MHz/5.06MHz)/2=29.64mです。
短縮率の66%を考慮すると、物理長は19.56mとなります。